Khi các bạn sinh viên sử dụng SPSS để làm báo cáo, nghiên cứu khoa học thì chắc hẳn phải sử dụng hồi quy đơn biến trong SPSS để dự báo, khảo sát. Vậy làm cách nào để chạy hồi quy đơn biến đạt kết quả cao? Hãy cùng chúng tôi tham khảo cách chạy chi tiết nhất ở bài viết dưới đây!

1. Hồi quy đơn biến trong SPSS là gì?
Hồi quy đơn biến trong SPSS là dạng hồi quy cơ bản trong hồi quy tuyến tính. Dùng để xác định mối quan hệ giữa một biến độc lập (biến giải thích) và một biến phụ thuộc. Hồi quy có ích chủ yếu trong tình huống mối quan hệ giữa hai biến không rõ ràng bằng mắt thường. Ví dụ, nó có thể được sử dụng để nghiên cứu tần suất các cuộc tấn công khủng bố ảnh hưởng như thế nào đến tăng trưởng kinh tế của các quốc gia trên thế giới……
Mục đích của hồi quy đơn biến trong SPSS là:
- Dùng để tìm hiểu, xác định mức độ ảnh hưởng của biến độc lập lên biến phụ thuộc
- Giải thích ý nghĩa của biến phụ thuộc đối với biến độc lập
- Dự đoán sự thay đổi của biến phụ thuộc theo biến độc lập
2. Cách chạy hồi quy đơn biến trong SPSS
Ví dụ: Một nhân viên bán hàng cho một hãng xe hơi lớn muốn xác định liệu có mối quan hệ giữa thu nhập của một cá nhân và mức giá họ trả cho một chiếc xe hơi hay không. Nhân viên muốn sử dụng thông tin này để xác định loại xe nào sẽ cung cấp cho khách hàng tiềm năng của mình trong tương lai.
Như vậy trong ví dụ trên, ta có thể xác định 2 yếu tố như sau:
- Thu nhập: Biến độc lập
- Mức giá: Biến phụ thuộc
– Chúng ta thực hiện hồi quy theo 4 bước như sau:
Bước 1: Ở thanh menu trên cùng, nhấp vào Analyze, sau đó chọn Regression, chọn Linear…

Khi đó bạn sẽ thấy một hộp thoại Hồi quy tuyến tính Linear Regression như sau:

Bước 2: Lúc này, bạn sử dụng mũi tên ở giữa hai cột để chuyển biến Income sang cột Biến độc lập – Independent(s), và biến Price vào cột Biến phụ thuộc – Dependent.
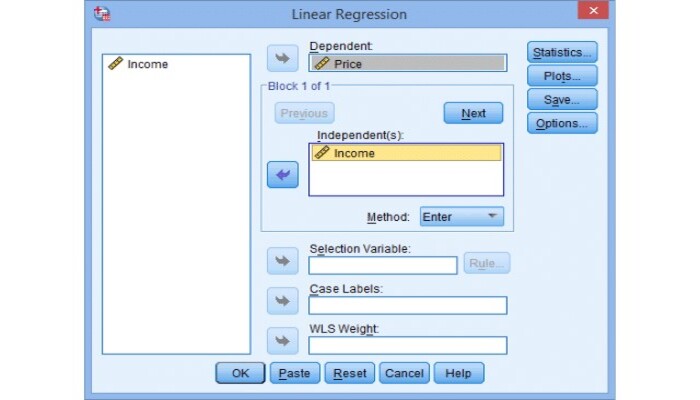
Bước 3: Điều chỉnh thông số phân tích bằng cách nhấn chọn Statistics và tích chọn các mục như hình sau. Sau khi hoàn tất bấm Continue.

Bước 4: Kiểm tra lại và nhấn OK để hệ thống cho ra kết quả

Khi tiến hành xử lý số liệu SPSS thì bạn thường phải trải qua nhiều khó khăn, trục trặc trong việc xử lý số liệu như dữ liệu cho kết quả xấu, chạy SPSS sai thao tác, không biết cách độc số liệu,…..Best4team có nhận xử lý số liệu SPSS để giải quyết những khó khăn đó cho các bạn, cam kết xử lý nhanh chóng, giao bài đúng hạn, dữ liệu không trùng lặp, cho kết quả đẹp nhất và đặc biệt cam kết bảo mật thông tin của khách hàng. Hãy tham khảo ngay!
3. Phân tích và đọc kết quả hồi quy đơn biến trong SPSS
Sau khi thực hiện xong các thao tác trên, phần mềm SPSS sẽ chạy phân tích và cho ra kết quả trong lần lượt 3 bảng sau:
– Bảng cần quan tâm đầu tiên là bảng Model Summary:
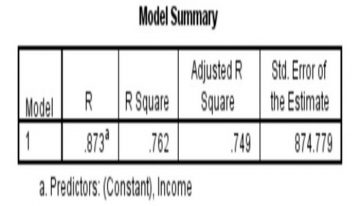
– Trong bảng này, ta đặc biệt chú ý đến 2 giá trị:
- R: Chỉ số này lớn hơn 0.5 chứng tỏ mô hình nghiên cứu là mô hình tốt. Trong ví dụ này, R = 0.873 chứng tỏ mô hình nghiên cứu được chấp nhận.
- R square: Đây là chỉ số cho biến mức độ mối tương quan giữa biến độc lập và biến phụ thuộc. Cụ thể, theo ví dụ trên, R square = 0.762, tức là biến độc lập được nghiên cứu ảnh hưởng 76,2% đến sự biến thiên của biến phụ thuộc, còn lại 23,8% là do các biến ngoài mô hình và sai số ngẫu nhiên.
– Bảng thứ hai hiện ra trong kết quả là bảng ANOVA, cho biết mức độ phù hợp của phương trình hồi quy với tập dữ liệu.

- Thông số cần quan tâm nhất trong bảng này là Sig. Nếu thông số này nhỏ hơn 05 (Sig. < 0.05) tức là mô hình hồi quy có độ phù hợp với dữ liệu.
- Trong ví dụ này, chỉ số = 0.000 < 0.05, tức là mô hình này có ý nghĩa thống kê, chứng tỏ mô hình hồi quy nghiên cứu phù hợp với tập dữ liệu phân tích.
– Cuối cùng là bảng Coefficients giúp ta xác định được phương trình hồi quy tuyến tính và đánh giá mức độ tác động của các biến độc lập với biến phụ thuộc.
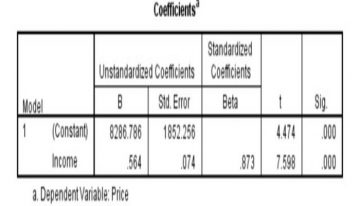
+ Lại một lần nữa để ý đến chỉ số Sig. trong bảng, nếu các chỉ số này đã nhỏ hơn 0.05 (Sig. < 0.05) tức là các biến nghiên cứu phù hợp, ta có thể chuyển đến bước tiếp theo.
+ Chú ý đến 2 cột B và Beta, đây chính là cột cho ra hệ số của các biến độc lập trong phương trình hồi quy tuyến tính với biến phụ thuộc. Cụ thể trong ví dụ trên, ta có thể dựa vào bảng viết được phương trình hồi quy tuyến tính như sau:
- Phương trình chuẩn tắc: Price = 873 x Income
- Phương trình chưa chuẩn tắc: Price = 8287 + 0.564 x Income
– Từ đó có thể biết, mức giá khách hàng chi ra để mua xe có tỷ lệ thuận với thu nhập của họ, cụ thể theo phương trình đã viết ở trên. Nhân viên bán hàng có thể dựa vào kết quả này để tối ưu hóa kế hoạch kinh doanh của mình.
– Lưu ý: Trong trường hợp phân tích hồi quy tuyến tính với nhiều biến độc lập, như ví dụ sau:
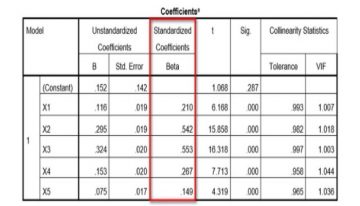
+ Ngoài chỉ số Sig., ta cần chú ý đến chỉ số VIF – chỉ số phản ánh hiện tượng đa cộng tuyến trong phương trình. Nếu chỉ số này lớn hơn 2 (VIF > 2) thì cần cẩn thận sẽ xảy ra hiện tượng đa cộng tuyến làm sai lệch đến kết quả.
+ Trong ví dụ trên, các chỉ số VIF đều thỏa mãn điều kiện, tức là không xảy ra hiện tượng đa cộng tuyến.
+ Bước tiếp theo cũng là viết phương trình hồi quy tuyến tính chuẩn tắc dựa vào cột Beta như sau:
Y = 0.21X1 + 0.542X2 + 0.553X3 + 0.267X4 + 0.149X5
- Dựa vào phương trình này, ta có thể đánh giá mức độ tác động từ mạnh đến yếu của biến độc lập vào biến phụ thuộc.
- Có thể thấy, trong phương trình trên, mức độ tác động từ mạnh đến yếu của các biến độc lập được xếp như sau: X2, X3, X4, X1, X5.
Để xử lý số liệu SPSS đạt kết quả cao đòi hỏi người làm phải hiểu biết được những thao tác cũng như có nhiều kinh nghiệm trong việc xử lý số liệu. Best4team sẽ hướng dẫn các bạn cách xử lý số liệu SPSS toàn tập, chi tiết nhất để các bạn có thể nắm được thật nhiều kiến thức áp dụng vào bài luận của mình. Hãy tham khảo ngay!
4. Sự khác biệt giữa hồi quy đơn biến và tương quan Pearson
Sự khác biệt giữa tương quan pearson và hồi quy đơn biến là một trong những câu hỏi thường gặp trong quá trình học tập, nghiên cứu của các bạn sinh viên. Hãy tham khảo biểu đồ so sánh dưới đây để thấy được sự khác biệt đó!
Biểu đồ so sánh
| Cơ sở để so sánh | Tương quan pearson | hồi quy đơn biến |
| Ý nghĩa | Tương quan là một thước đo thống kê xác định mối quan hệ đồng hoặc liên kết của hai biến. | Hồi quy mô tả cách một biến độc lập có liên quan về số với biến phụ thuộc. |
| Sử dụng | Để biểu diễn mối quan hệ tuyến tính giữa hai biến. | Để phù hợp với một dòng tốt nhất và ước tính một biến trên cơ sở của một biến khác. |
| Biến phụ thuộc và độc lập | Không khác nhau | Cả hai biến đều khác nhau. |
| Chỉ ra | Hệ số tương quan chỉ ra mức độ mà hai biến di chuyển cùng nhau. | Hồi quy cho thấy tác động của một thay đổi đơn vị trong biến đã biết (x) đến biến ước tính (y). |
| Mục tiêu | Để tìm một giá trị số biểu thị mối quan hệ giữa các biến. | Để ước tính các giá trị của biến ngẫu nhiên trên cơ sở các giá trị của biến cố định.
|
Như vậy, bài viết trên đã hướng dẫn cách chạy hồi quy đơn biến trong SPSS chi tiết từ A – Z, chi tiết nhất toàn tập có ví dụ, hinh ảnh minh họa cụ thể, đồng thời giúp chúng ta hiểu được khái niệm, mục đích của hồi quy đơn biến, cách đọc kết quả phân tích cũng như tìm hiểu sự khách biệt giữa tương quan và hồi quy. Hy vọng các bạn thành công áp dụng vào bài nghiên cứu khoa học của mình. Chúc các bạn đạt kết quả cao!
Theo: Ngọc Yến – Ecci



Để lại một bình luận